在数学的浩瀚宇宙中,定理证明一直是一项极具挑战性的任务。如今,随着人工智能技术的飞速发展,我们迎来了一款强大的定理证明工具——Goedel-Prover-V2。这款由普林斯顿大学、清华大学以及英伟达等顶尖机构联合推出的开源模型,正在为数学研究和相关领域的探索带来前所未有的突破。Goedel-Prover-V2 究竟有何独特之处?它又将如何改变我们对数学证明的认知?本文将深入剖析其技术原理、性能表现以及潜在的应用场景,带您领略这款 AI 定理证明器的强大魅力。
Goedel-Prover-V2:数学证明的新里程碑
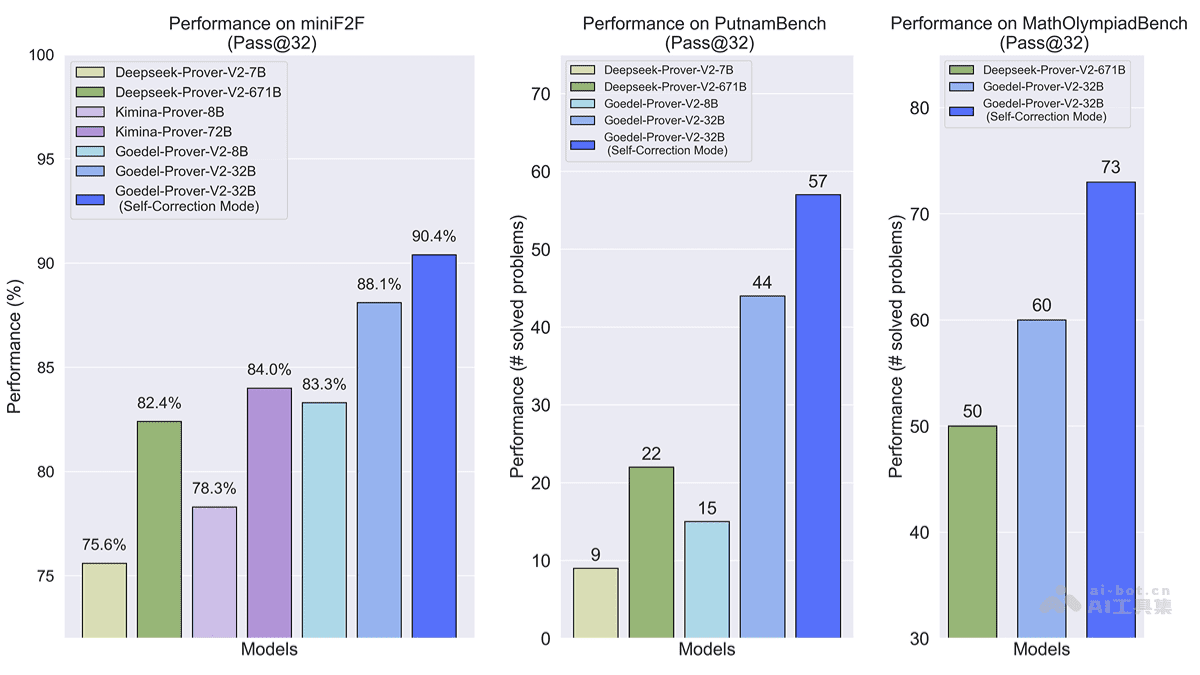
Goedel-Prover-V2 并非横空出世,而是站在前人研究的肩膀上,实现了质的飞跃。它通过分层式数据合成、验证器引导的自我修正以及模型平均等创新技术,显著提升了自动形式化证明生成的性能。更令人瞩目的是,该模型提供了两个参数版本:32B 和 8B。其中,32B 模型在 MiniF2F 基准测试中取得了 90.4% 的 Pass@32 成绩,一举超越了参数量高达 671B 的 DeepSeek-Prover-V2。此外,Goedel-Prover-V2 还在 PutnamBench 和 MathOlympiadBench 基准测试中名列前茅,充分展现了其卓越的定理证明能力。
这一成就的取得,无疑为 AI 在数学定理证明领域的研究树立了新的标杆。它不仅证明了 AI 在复杂数学问题求解方面的巨大潜力,也为未来的研究方向提供了新的思路。
Goedel-Prover-V2 的核心功能
Goedel-Prover-V2 的强大功能,是其在定理证明领域取得成功的关键。以下是其几个主要功能:
自动生成证明:Goedel-Prover-V2 能够为复杂的数学问题自动生成形式化的证明,这极大地减轻了数学家们繁琐的证明工作,使他们能够将更多精力投入到问题的思考和创新上。
自我修正能力:模型能够根据 Lean 编译器的反馈,迭代修正自身的证明,从而不断提高证明的质量。这种自我修正的能力,使其能够适应各种复杂的数学问题,并逐步逼近最优解。
高效训练与优化:Goedel-Prover-V2 采用了分层式数据合成和模型平均等技术,有效提升了训练效率和模型性能。这些技术的应用,使其能够在较短的时间内训练出高性能的模型,并保持模型的稳定性和可靠性。
开源与可扩展性:Goedel-Prover-V2 提供了开源模型和数据集,这为研究者们进一步开发和改进提供了便利。开源的特性,使其能够吸引更多的研究者参与其中,共同推动定理证明技术的发展。
Goedel-Prover-V2 的技术原理
要理解 Goedel-Prover-V2 的强大之处,深入了解其背后的技术原理至关重要。以下将详细介绍其三大核心技术:分层式数据合成、验证器引导的自我修正以及模型平均。
- 分层式数据合成(Scaffolded Data Synthesis):
分层式数据合成是 Goedel-Prover-V2 的一项关键创新。它通过自动生成难度逐步递增的证明任务,帮助模型从简单问题逐步过渡到复杂问题。这种循序渐进的学习方式,更符合人类的学习规律,能够有效地提高模型的学习效率和泛化能力。
具体来说,分层式数据合成首先会生成一些简单的证明问题,然后逐步增加问题的难度,最终生成一些非常复杂的证明问题。模型在解决这些问题的过程中,能够不断学习和掌握新的知识和技能,从而逐步提高其定理证明能力。同时,该技术基于生成中级难度的问题,填补简单问题和复杂问题之间的空白,提供更密集的训练信号,让模型能够更好地理解和掌握证明的内在逻辑。

- 验证器引导的自我修正(Verifier-Guided Self-Correction):
验证器引导的自我修正是 Goedel-Prover-V2 的另一项重要技术。模型通过 Lean 编译器的反馈,学习如何迭代修正自身的证明。Lean 编译器是一种形式化验证工具,可以对证明的正确性进行严格的验证。通过与 Lean 编译器的交互,模型能够及时发现和纠正证明中的错误,从而提高证明的准确性和可靠性。
这种自我修正的过程,高度模拟了人类在完善证明时的修正过程。当数学家在证明一个定理时,往往需要经过多次尝试和修改,才能最终得到正确的证明。Goedel-Prover-V2 通过验证器引导的自我修正,使其能够像人类一样,不断完善自身的证明,最终达到最优的证明效果。
- 模型平均(Model Averaging):
模型平均是一种集成学习技术,通过平均多个模型的预测结果,来提高整体的性能。Goedel-Prover-V2 基于平均多个训练阶段的模型检查点,恢复模型的多样性。这种方法可以有效地减少模型的方差,提高模型的鲁棒性和泛化能力。
在实际应用中,模型平均可以在更大的 Pass@K 值下显著提升模型的整体性能。这意味着,模型在解决多个问题时,能够取得更好的平均成绩。这对于实际应用来说,是非常重要的。因为在实际应用中,我们往往需要模型能够解决各种各样的问题,而不是仅仅在个别问题上表现出色。
Goedel-Prover-V2 的卓越性能
Goedel-Prover-V2 在多个基准测试中都取得了优异的成绩,充分证明了其卓越的性能。以下将详细介绍其在 MiniF2F、PutnamBench 和 MathOlympiadBench 等基准测试中的表现。
- MiniF2F 基准测试:
MiniF2F 是一个常用的形式化证明基准测试,用于评估模型在解决复杂数学问题方面的能力。Goedel-Prover-V2 在该基准测试中取得了令人瞩目的成绩。
32B 模型:
- Pass@32:达到了 90.4%,显著优于 DeepSeek-Prover-V2-671B 的 82.4%。这表明,Goedel-Prover-V2 在解决复杂数学问题方面的能力已经超越了目前最先进的模型。
- 自校正模式:在自校正模式下,Pass@32 成绩进一步提升至 90.4%。这表明,通过自我修正,模型能够进一步提高其证明的准确性和可靠性。
8B 模型:
- Pass@32:达到了 83.3%,与 DeepSeek-Prover-V2-671B 的 82.4% 相当,但模型规模小了近 100 倍。这表明,Goedel-Prover-V2 在保持高性能的同时,也具有较高的效率。
- PutnamBench 基准测试:
PutnamBench 是一个用于评估模型在解决数学竞赛问题方面的能力的基准测试。Goedel-Prover-V2 在该基准测试中同样表现出色。
32B 模型:
- Pass@64:解决了 64 个问题,位居榜首。这表明,Goedel-Prover-V2 在解决数学竞赛问题方面的能力非常强大。
- Pass@32:解决了 57 个问题,显著优于 DeepSeek-Prover-V2-671B 的 47 个问题。这进一步证明了 Goedel-Prover-V2 在解决复杂数学问题方面的优势。
8B 模型:
- Pass@32:表现也十分出色,与 DeepSeek-Prover-V2-671B 相当。这表明,即使是较小规模的模型,也能够取得优异的成绩。
- MathOlympiadBench 基准测试:
MathOlympiadBench 是一个用于评估模型在解决奥林匹克数学竞赛问题方面的能力的基准测试。Goedel-Prover-V2 在该基准测试中同样取得了优异的成绩。
- 32B 模型:解决了 73 个问题,显著优于 DeepSeek-Prover-V2-671B 的 50 个问题。这表明,Goedel-Prover-V2 在解决奥林匹克数学竞赛问题方面的能力非常强大。
- 8B 模型:表现也非常接近,展现了强大的定理证明能力。这表明,即使是较小规模的模型,也能够在奥林匹克数学竞赛问题中取得不错的成绩。
Goedel-Prover-V2 的广泛应用场景
Goedel-Prover-V2 的应用前景十分广阔。除了数学研究之外,它还可以在软件和硬件验证、教育、人工智能与机器学习以及科学研究与工程等领域发挥重要作用。
- 数学定理证明:
Goedel-Prover-V2 可以自动生成数学定理的形式化证明,帮助数学家验证猜想、探索新的数学理论,加速数学研究的进程。这将极大地提高数学研究的效率,并可能带来新的数学发现。
- 软件和硬件验证:
在软件开发和硬件设计中,Goedel-Prover-V2 可以用于验证算法、程序逻辑和电路设计的正确性。通过形式化证明,可以确保软件和硬件系统的可靠性,减少错误和漏洞,提高系统的安全性。这对于开发高质量的软件和硬件系统至关重要。
- 教育:
Goedel-Prover-V2 可以作为数学教育的辅助工具,为学生提供形式化证明的示例,帮助他们更好地理解和掌握数学概念和定理。通过观察和学习 Goedel-Prover-V2 生成的证明,学生可以更深入地理解数学的本质,并提高他们的数学能力。
- 人工智能与机器学习:
在人工智能和机器学习领域,Goedel-Prover-V2 可以用于验证模型的数学基础和算法逻辑,确保模型的可靠性和准确性。这对于开发可靠的人工智能系统至关重要。
- 科学研究与工程:
Goedel-Prover-V2 可以用于验证科学研究中的数学模型和理论,帮助科学家和工程师确保设计方案的可行性和可靠性。这对于科学研究和工程实践具有重要意义。
结语
Goedel-Prover-V2 的推出,无疑为 AI 在数学定理证明领域的研究注入了新的活力。它的强大功能、卓越性能以及广泛应用场景,使其成为数学研究和相关领域不可或缺的工具。随着 AI 技术的不断发展,我们有理由相信,Goedel-Prover-V2 将在未来的数学研究中发挥更加重要的作用,并为我们带来更多的惊喜。