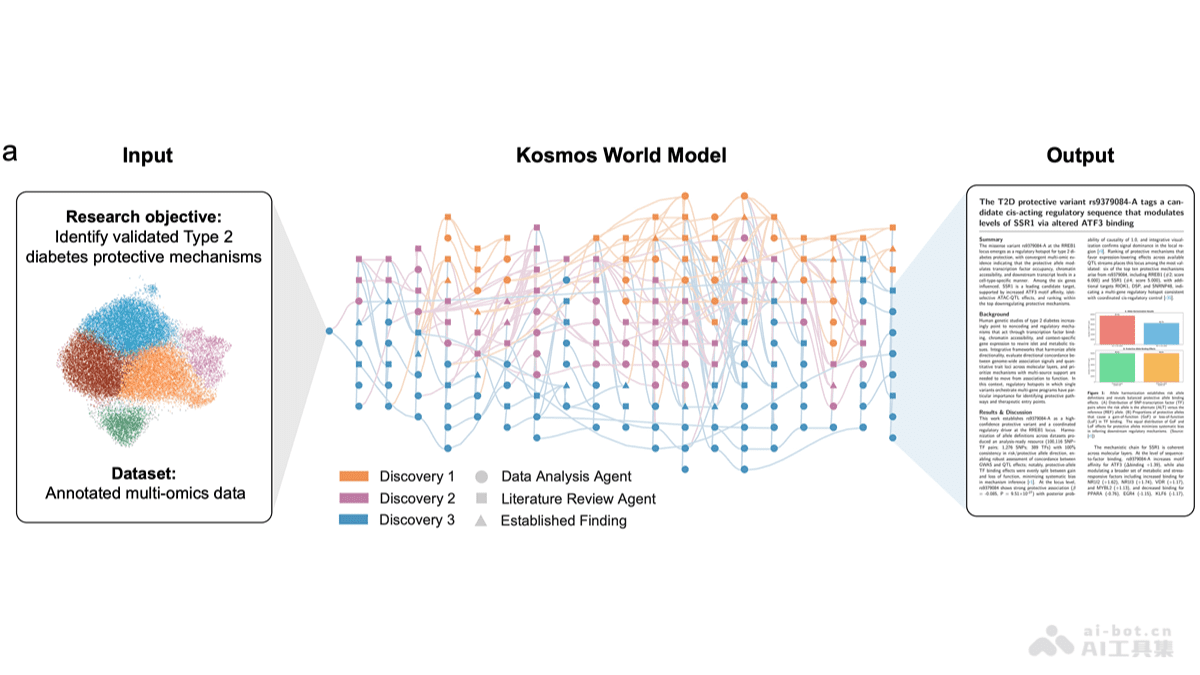
荷兰版画大师M.C. 埃舍尔的艺术作品以其对视错觉和不可能结构的精妙呈现,为我们打开了一扇通往多维空间感知世界的大门。他的画作中充斥着“不可能物体”,这些构造在物理法则下显得矛盾重重,却又在视觉上令人信服。例如,一幅画中看似向上行走的楼梯,仅需转换视角,便可能向下延伸,这种空间扭曲的魅力正是埃舍尔作品的核心所在。
长期以来,计算机图形学领域的科学家和设计师在尝试重现这些视错觉时,往往面临着巨大的挑战。传统的三维建模方法通常只能通过弯曲或切割实际形状,并将其置于特定角度来模拟此类效果。然而,这种“曲线救国”的方式存在显而易见的局限性:一旦改变结构的平滑度或光照条件,其作为视错觉的本质就会被揭示,导致其无法用于精确的几何学问题分析或计算。
麻省理工学院计算机科学与人工智能实验室(CSAIL)的研究人员另辟蹊径,提出了一种革新性的方法来表示“不可能物体”。他们开发的创新工具“Meschers”能够将二维图像和三维模型转化为2.5维结构,从而创建出类似埃舍尔风格的窗户、建筑甚至是甜甜圈等视觉错觉。这种突破性的方法允许用户在保持原始视错觉完整性的同时,对独特的几何结构进行重新打光、平滑处理和深入研究,极大地拓宽了数字内容创作的可能性。
这一工具的问世,对几何学研究者而言意义非凡。它能辅助他们精确计算弯曲“不可能表面”上两点之间的最短路径(即“测地线”),以及模拟热量在这些非传统结构上的扩散方式(“热扩散”)。对于艺术家和计算机图形学专家来说,Meschers则提供了一个强大的平台,使他们能够在多个维度上创造出突破物理定律的设计,从而以前所未有的自由度表达创意。
项目主要负责人、麻省理工学院博士生Ana Dodik致力于设计不受现实物理限制的计算机图形工具,旨在让艺术家能够独立于形状的物理可实现性来表达其意图。她指出:“借助Meschers,我们为艺术家们解锁了一类全新的计算机可操作形状。这些形状还能帮助感知科学家理解物体何时真正变得‘不可能’的临界点。”这一愿景预示着计算机图形学将从模拟现实转向创造现实,甚至超越现实。
探究“不可能物体”的本质与Meschers的原理
“不可能物体”之所以“不可能”,在于它们无法在真实的三维空间中完全构建。它们的各个组成部分在局部看来是合理的,但当尝试将其整合为一个整体时,却无法正确地“粘合”在一起。然而,正如CSAIL研究人员所发现的,计算上可以模仿的,恰恰是我们感知这些形状的过程。
以著名的“潘洛斯三角”(Penrose Triangle)为例,这个整体在物理上是不可能存在的,因为其深度无法“累加”。但我们依然能够识别出它内部的真实三维形状,例如其三个L形的角。这些局部区域在三维空间中是可实现的——这一特性被称为“局部一致性”——但当我们试图将它们组装起来时,它们却无法形成一个全局一致的形状。Meschers方法的精妙之处在于,它建模了这些局部一致的区域,却不强制它们必须全局一致,从而巧妙地拼接出埃舍尔风格的结构。
在技术层面,Meschers在幕后将“不可能物体”表示为我们已知其图像中的x和y坐标,以及相邻像素之间z坐标(深度)的差异。该工具正是利用这些深度差异来间接推断和操作“不可能物体”的。这种基于差异的建模方式,巧妙地绕过了传统三维建模中对全局一致性的严格要求,使得对这些违背直觉的几何体进行计算和编辑成为可能。

Meschers的多功能应用场景
Meschers的功能远不止渲染“不可能物体”那么简单。它还能将这些复杂结构细分为更小的形状,从而实现更精确的几何计算和平滑操作。这一过程使得研究人员能够有效减少“不可能形状”的视觉缺陷,例如他们成功将一个原本粗糙的红色心形轮廓平滑细化。
研究团队还将Meschers应用于一个“不可能的百吉饼”(impossibagel)模型,其中百吉饼以一种物理上不可能的方式进行了阴影处理。Meschers协助Dodik和她的同事模拟了热扩散过程,并计算了模型不同点之间的测地距离。
Dodik解释道:“想象你是一只蚂蚁,正在这个百吉饼上爬行,你想要知道需要多久才能穿越它。同样地,我们的工具可以帮助数学家近距离分析‘不可能形状’的底层几何结构,就像我们研究现实世界的物体一样。”这展示了Meschers在纯数学和应用几何领域研究的巨大潜力,尤其是在处理那些超越传统欧几里得几何范畴的问题时。
Meschers就像一位魔术师,能够将看似普通的物体转化为奇妙的视错觉,极大地便利了计算机图形艺术家创作“不可能物体”的过程。它还能利用“逆向渲染”工具,将“不可能物体”的绘画和图像转化为高维度的设计,从而为现有艺术作品注入新的数字生命,并探索其在数字空间中的更多可能性。
资深作者、电气工程与计算机科学副教授、CSAIL几何数据处理小组负责人Justin Solomon强调:“Meschers证明了计算机图形工具不必受物理现实规则的约束。令人难以置信的是,艺术家们利用Meschers可以推断出那些在现实世界中永远无法找到的形状。”这一声明不仅是对Meschers能力的肯定,也为计算机图形学领域的未来发展指明了方向:一个更加自由、更具想象力的创作空间。
Meschers的这种多功能性还体现在它能够帮助计算机图形艺术家调整其创作作品的阴影效果,同时完整保留视错觉。这种能力使得创作者可以根据需要改变艺术作品的光照,以描绘更丰富的场景,例如从日出到日落的不同光线效果。Meschers通过重新打光一个滑板上的狗狗模型,有力地证明了这一点,展示了其在艺术表现力上的巨大提升。
未来的展望:Meschers的持续进化
尽管Meschers已展现出强大的功能和广泛的应用前景,但对于Dodik和她的团队来说,这仅仅是一个开始。当前,他们正在考虑设计一个更直观的用户界面,以使Meschers更易于操作,并构建更复杂的场景。此外,他们还在与感知科学家紧密合作,探索如何更广泛地应用这一计算机图形工具。
这种跨学科的合作至关重要。通过与感知科学家的交流,研究团队有望更深入地理解人类视觉系统如何处理和解释这些“不可能”的几何结构。这不仅有助于完善Meschers的算法和功能,也可能为认知科学领域带来新的启示,例如关于大脑如何构建和识别空间信息的研究。Meschers的未来发展方向清晰而充满潜力,它将持续推动计算机图形学与人类感知的边界,为数字时代的创新带来无限可能。