在当前人工智能技术的飞速发展浪潮中,大型语言模型(LLMs)的综合能力已成为衡量其先进性的关键指标,而其中,数学与代码推理能力更是被视为评估模型“智能”深度的试金石。这些能力不仅关乎模型能否理解并执行复杂逻辑指令,更直接影响其在科学研究、工程开发及金融分析等高精度领域的应用潜力。近年来,众多科技巨头与研究机构纷纷投入巨资,致力于提升LLMs在这些专业领域的表现。正是在这一背景下,快手公司凭借其前瞻性的技术布局与深厚的研发实力,推出了一款基于Qwen3-8B-Base架构的创新性模型——Klear-Reasoner。该模型一经发布便引起了业界的广泛关注,其在多项权威基准测试中展现出卓越性能,尤其在数学推理方面,准确率更是突破了90%大关,使其在同等规模的模型中脱颖而出,树立了新的行业标杆。
Klear-Reasoner的成功并非偶然,而是得益于其核心算法的创新突破——梯度保持裁剪策略优化(GPPO,Gradient-Preserving Clipping Policy Optimization)算法。这一算法是强化学习领域的一次重要进步,它巧妙地解决了传统训练策略中长期存在的“保守性”问题。传统的梯度裁剪方法虽然能够有效防止模型在训练过程中因梯度爆炸而导致的不稳定,但其副作用是可能裁剪掉那些看似微小却至关重要的梯度信息,从而限制了模型的探索空间,使其在面对新颖或复杂问题时显得过于保守,难以跳出局部最优解。GPPO算法则通过一种更为精妙和“温和”的机制,确保了在反向传播过程中,所有梯度信息都能得到有效利用,即便是那些可能导致较大更新的梯度,也能够以一种受控的方式参与到模型的权重调整中。这意味着GPPO在维持训练过程高度稳定性的同时,极大地拓宽了模型的探索边界,使其能够更积极地尝试不同的解决方案,从而更快地识别并修正错误。这种平衡了稳定性和探索性的设计,是Klear-Reasoner能够在复杂数学推理任务中取得突破性进展的关键因素。
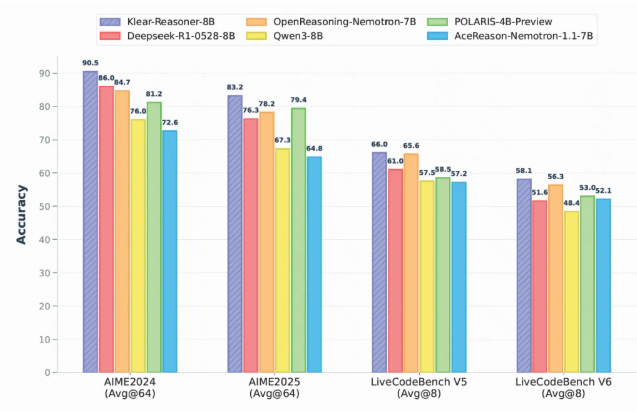
Klear-Reasoner的卓越性能并非纸上谈兵,而是在一系列严格的基准测试中得到了充分验证。在被视为高难度数学推理能力试金石的AIME2024测试中,Klear-Reasoner取得了令人瞩目的90.5%高分,这一成绩不仅远超同规模的多数开源模型,更彰显了其在处理复杂、多步骤数学问题上的深厚潜力。即使在挑战性更高的AIME2025测试中,该模型也稳定保持了83.2%的优秀准确率。这些数据强有力地证明了Klear-Reasoner在数学推理领域的技术领先地位。Klear团队在模型发布的同时,慷慨地分享了其详细的训练流程与关键策略,为整个AI社区提供了宝贵的经验。他们强调了数据质量在训练中的核心地位,指出即便在高难度的样本集中,也应有策略地保留一定比例的“错误”样本,因为这些错误恰恰是模型学习和提升泛化能力的关键点。此外,团队还特别指出,在强化学习阶段采用“软奖励”(Soft Rewards)策略,相比传统的“硬奖励”(Hard Rewards)能更有效地提升模型的学习效率和稳定性。软奖励通过提供更精细的反馈信号,允许模型在探索过程中进行小步调整,避免了因“非黑即白”的硬性惩罚而导致的训练震荡,从而加速了模型对知识的吸收和整合。
值得深入探讨的是Klear团队在数据处理和奖励机制上的独到见解。他们在实验中反复印证了一个关键结论:优质数据的价值往往超越了单纯的数量堆砌。这意味着,在监督微调(SFT)阶段,与其盲目追求庞大的数据集,不如将精力集中于对数据进行精细化筛选与去噪。通过严格过滤掉低质量、噪声大或标注错误的样本,并专注于那些结构清晰、逻辑严谨、高质量的样本进行训练,能够显著提升模型的训练效率与最终性能。这一策略不仅节省了计算资源,更关键的是确保了模型在学习初期就能接触到正确的模式和逻辑,为其后续的强化学习阶段奠定了坚实的基础。此外,关于软奖励策略的应用,Klear团队的实践也为我们提供了新的启示。传统的硬奖励(如二元的是非判断)可能导致模型在早期训练中面临“探索-惩罚”的困境,使其在寻找最优解时过于谨慎。而软奖励则能够提供一个连续的、梯度化的反馈信号,即使是“不那么完美”的中间步骤也能获得部分奖励,这鼓励了模型更大胆地探索解决方案空间,并在每次尝试中学习到更多有价值的信息,从而加速了收敛过程,并增强了模型面对复杂环境的适应性和鲁棒性。
Klear-Reasoner模型的成功发布,不仅仅是快手公司在人工智能领域技术实力的一次集中展示,更重要的是,它为业界提供了一条可复现且高效的推理模型训练路径。这一成果为未来的LLM研究和开发指明了方向,尤其是在如何平衡模型探索能力与训练稳定性、以及如何精细化数据处理与奖励机制方面,提供了宝贵的实践经验和理论依据。它预示着,随着对核心算法和训练策略的持续优化,LLMs在处理复杂逻辑推理任务上的表现将达到前所未有的高度。展望未来,Klear-Reasoner所代表的这类高精度推理模型,有望在更多专业领域发挥关键作用,例如在辅助科学家进行复杂理论推导、帮助工程师优化代码逻辑、乃至在金融市场中进行风险评估和趋势预测等方面,提供前所未有的智能辅助,从而共同推动人工智能技术迈向一个更加精准、高效的新阶段。