在人工智能领域,DeepMind再次取得突破性进展,其最新研发的AlphaProof系统在国际数学舞台上展现了令人瞩目的能力。这一AI系统不仅在数学证明领域实现了重大突破,更在2024年国际数学奥林匹克(IMO)中取得了与银牌得主相当的成绩,距离金牌仅一步之遥。这一成就标志着人工智能在数学推理能力上的显著飞跃,同时也引发了关于AI如何重塑数学研究格局的深度思考。
从计算到理解:数学AI的进化之路
长期以来,计算机在数学领域主要扮演高效计算工具的角色。它们能够以惊人速度完成复杂运算,却从未真正威胁到人类数学家的地位。直到最近,AI系统在高中级别的数学竞赛中表现依然平平。DeepMind的AlphaProof彻底改变了这一现状。
"计算机极其擅长处理数字,但它们并没有让多少人类数学家失业。"这一局面正在被AlphaProof改写。该系统不仅在2024年国际数学奥林匹克竞赛中取得了银牌级别的成绩,还在世界最负盛名的大学生数学竞赛中仅差一分即可获得金牌。
真正的理解:超越表面计算
传统计算机在数学竞赛中表现不佳的原因在于,虽然它们在计算能力上远超人类,但在高级数学所需的逻辑和推理方面却相对薄弱。简单来说,计算机擅长快速执行计算,但通常不理解为何要进行这些计算。
DeepMind的研究人员Thomas Hubert指出:"伯特兰·罗素曾出版了一本500页的《数学原理》来证明1+1=2。"这一例子生动说明了数学证明的深度和复杂性。数学家构建证明的方式、推导结论所需的步骤以及这些步骤的巧妙设计,都体现了人类的智慧、创造力和数学美感。
AlphaProof的诞生旨在让AI达到这种深层次的数学理解。这一旅程始于解决AI训练数据匮乏的普遍问题。
数学问题翻译器:跨越形式化障碍
像ChatGPT这样由大型语言模型驱动的AI系统从海量文本中学习,其中包括数学相关的教科书和著名数学家的著作。因此,它们在证明数学命题方面取得了一定成功。然而,这些系统的推理本质上是统计性的,只能返回"听起来正确"的答案,而非保证绝对正确性。
DeepMind需要的是能够"真正正确"而非"听起来正确"的AI,这要求构建一个全新的、更加形式化的训练环境。为此,团队采用了名为Lean的软件包。
Lean是一款帮助数学家编写精确定义和证明的计算机程序,它依赖一种精确的形式化编程语言(同样称为Lean),数学命题可以被翻译成这种语言。一旦形式化的命题被上传到程序中,它就能检查其正确性,并给出"正确"、"缺少内容"或"使用了未经证明的事实"等反馈。
然而,网上大多数数学命题和证明都是用自然语言编写的,而用Lean编写的数量极为有限。"使用形式化语言的主要困难在于数据量非常少,"Hubert表示。
为解决这一问题,研究人员训练了一个Gemini大型语言模型,将数学命题从自然语言翻译成Lean。这个模型充当自动形式化工具,生成了约8000万条形式化的数学命题。
虽然翻译并不完美,但团队巧妙地利用了这一点:"有很多方法可以利用近似翻译,"Hubert声称。
学习思考:AlphaProof的技术架构
DeepMind为AlphaProof设计的灵感来源于其AlphaZero系统——这款AI曾在国际象棋、围棋和将棋等棋类游戏中取得突破性成功。在团队看来,在Lean和一般数学中构建证明不过是另一个需要掌握的"游戏"。
"我们试图通过反复试验来学习这个游戏,"Hubert解释道。形式化不完善的问题为系统提供了大量犯错和学习的宝贵机会。在训练阶段,AlphaProof只是证明或反驳其数据库中的问题。如果某个问题的翻译质量不佳,识别出这种不正确性本身就是一种有用的锻炼。
与AlphaZero类似,AlphaProof主要由两个核心组件构成:
大型神经网络:拥有数十亿参数,通过反复试验学习在Lean环境中工作。每当成功证明或反驳一个命题时,系统会获得奖励;而每进行一次推理步骤则受到惩罚,这种机制鼓励生成简短、优雅的证明。
树搜索算法:探索每一步可能采取的所有行动,推动证明向前发展。由于数学中可能的行动数量近乎无限,神经网络负责查看搜索树中的可用分支,并将计算资源仅分配给最有希望的分支。
经过几周训练,系统在大多数基于高中竞赛问题的数学竞赛基准测试中表现出色,但在最困难的问题上仍显不足。为解决这一挑战,团队添加了第三个组件——这是AlphaZero乃至其他AI系统中都没有的创新。
人性火花:测试时强化学习(TTRL)
第三个组件被称为测试时强化学习(TTRL),它大致模拟了数学家处理最困难问题的方式。学习过程同样依赖于神经网络和搜索树算法的组合,区别在于学习来源。
在TTRL模式下,AlphaProof不再依赖广泛的形式化问题数据库,而是基于当前正在处理的问题生成全新的训练数据集。这一过程涉及创建原始命题的无数变体——有些稍微简化,有些更一般化,有些则与原命题仅有松散联系。系统随后尝试证明或反驳这些变体。
这大致相当于人类面对特别难题时的策略:"我不太明白,所以先尝试一个更简单的版本来练习。"这种即时学习机制效果惊人。
在2024年国际数学奥林匹克竞赛中,共有42分(六个各7分的问题)。获得金牌需要29分或以上(共有58人达到),银牌奖授予获得22-28分的参赛者(共123人)。问题难度各异,第六题作为"最终Boss"是最难的,只有六名参赛者成功解答。AlphaProof成为第七个解决该问题的"选手"。
优化创新:AlphaProof的局限与挑战
尽管AlphaProof取得了令人瞩目的成绩,但它并非全能的数学天才。其"银牌"背后付出了相当大的代价——不仅是字面意义上的,也是比喻意义上的。
首先,AlphaProof并非完全独立工作。人类必须先将问题转化为Lean兼容格式,软件才能开始处理。在六个奥林匹克问题中,第四题涉及几何,而AI在这方面并未优化。为此,AlphaProof需要调用名为AlphaGeometry 2的几何专业AI助手,后者在几分钟内轻松解决了该问题。单独计算,AlphaProof得分为21分而非28分,理论上应获得铜牌而非银牌。
其次,人类参赛者需要在两个各4.5小时的会期内解决六个问题,而AlphaProof则使用多个张量处理单元(TPU)全力运转数天才完成。最耗时和耗能的组件是TTRL,它在解决三个问题时每个都花费了三天时间。如果AlphaProof与人类参赛者采用相同标准,它基本上会耗尽时间;如果不是诞生于价值数千亿美元的科技巨头,它也会耗尽资金。
研究团队在论文中承认,运行AlphaProof的计算要求对大多数研究机构和有抱负的数学家来说可能是成本过高的。AI应用中的计算能力通常以TPU-天(即张量处理单元全天候运行一天)来衡量,而AlphaProof每个问题就需要数百TPU-天。
此外,国际数学奥林匹克竞赛是高中水平的比赛,尽管问题确实困难,但仍基于数学家已知的知识。研究级别的数学需要发明全新概念,而不仅仅是处理现有概念。
未来展望:从竞赛到研究
尽管面临挑战,DeepMind相信可以克服这些障碍,优化AlphaProof使其资源消耗更低。"我们不想止步于数学竞赛,"Hubert表示,"我们希望构建一个能够真正贡献于研究级数学的AI系统。"
他的目标是让AlphaProof对更广泛的研究社区可用。"我们还将发布一种AlphaProof工具,"他补充道,"这将是一个小型可信测试者项目,以验证这对数学家是否有用。"
AlphaProof的突破不仅展示了AI在数学推理方面的潜力,也为未来AI与数学家的协作模式提供了启示。想象一下,AI能够处理繁琐的形式化工作,提出创新性思路,而人类数学家则专注于更高层次的创造性思维和概念突破。这种协作模式可能会加速数学发现的进程,解决当前人类难以企及的复杂问题。
技术细节:AlphaProof如何工作
深入理解AlphaProof的技术架构,有助于我们把握其创新之处和局限性。该系统的核心在于将数学证明问题转化为一种"游戏",通过强化学习来掌握。
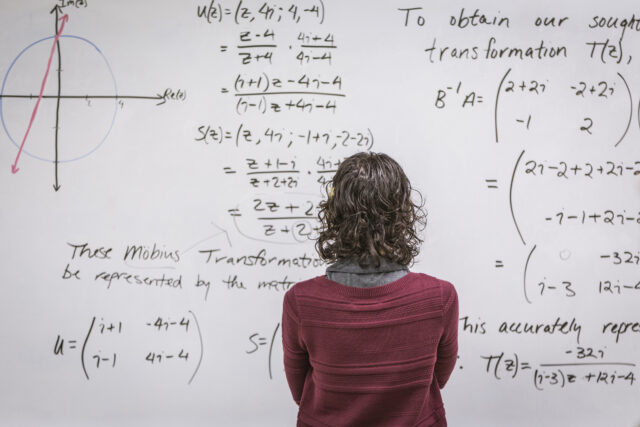
形式化语言的重要性
Lean的形式化语言为AlphaProof提供了精确的推理基础。与自然语言相比,形式化语言消除了歧义,确保每一步推理都有严格定义。这种精确性对于数学证明至关重要,因为数学真理建立在严密的逻辑链条上。
"形式化语言就像数学的编程语言,"Hubert解释道,"它允许我们以机器可验证的方式表达数学思想。"
神经网络与搜索的协同
AlphaProof的神经网络负责评估证明策略的质量,而树搜索算法则探索具体的证明路径。这种组合既保证了探索的广度,又确保了效率。
"神经网络就像一位经验丰富的数学家,能够直觉地判断哪些证明方向更有希望,"Hubert比喻道,"而搜索算法则像是一位勤奋的学生,系统地尝试这些方向。"
测试时强化学习的创新
TTRL组件是AlphaProof最创新的部分。它使系统能够在遇到新问题时即时生成训练数据,这种能力类似于人类在面对陌生问题时采取的简化策略。
"TTRL让AlphaProof能够像人类一样,通过解决简化版本来学习解决复杂问题,"Hubert指出,"这是传统AI系统难以做到的。"
数学自动化的历史与未来
AlphaProof的成就建立在数学自动化研究的长期积累之上。从20世纪50年代开始,计算机辅助证明就成为计算机科学的重要研究方向。
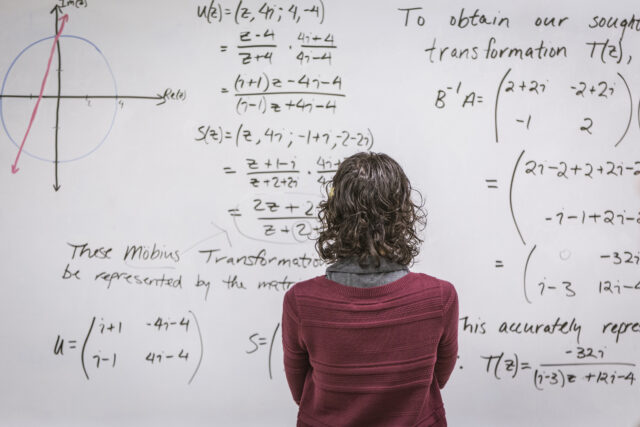
早期尝试
早期的数学自动化系统如AUTOMATH和Mizar主要关注形式化数学基础。这些系统能够验证已经写好的证明,但缺乏自主发现新证明的能力。
机器学习时代的转变
随着机器学习技术的发展,特别是深度学习的兴起,数学AI开始展现出新的可能性。AlphaProof代表了这一领域的最新进展,它不仅能够验证证明,还能自主发现新的证明路径。
从竞赛到研究的跨越
AlphaProof在IMO中的成功只是开始。DeepMind的最终目标是开发能够协助研究级数学工作的AI系统。这将需要解决几个关键挑战:
- 计算效率:当前系统需要大量计算资源,需要优化以降低成本。
- 概念创新:研究级数学需要发明全新概念,而不仅仅是应用现有知识。
- 人机协作:开发AI与数学家有效协作的界面和工作流程。
对数学研究的影响
AlphaProof的出现将对数学研究产生深远影响,从多个方面改变数学家的日常工作方式。
证明验证与发现
AI系统能够快速验证复杂证明的正确性,大幅减少人工检查的时间。同时,它们还能提出人类可能忽略的证明路径,带来新的见解。
教育与研究平衡
对于数学教育,AI工具可以帮助学生理解证明结构,提供个性化指导。对于研究,AI可以处理繁琐的计算和形式化工作,让数学家专注于创造性思维。
跨学科融合加速
数学AI的发展将促进数学与其他学科的融合,特别是在需要复杂推理的领域如理论物理、计算机科学和经济学。
伦理与哲学思考
AlphaProof的进步也引发了一系列伦理和哲学问题,值得我们深思。
数学本质的再思考
如果AI能够解决复杂的数学问题,这是否意味着数学不仅仅是人类创造力的产物?数学真理是否独立于人类思维而存在?这些问题挑战了我们对数学本质的传统理解。
人类独特性的重新定义
随着AI在包括数学在内的认知领域取得进展,我们需要重新思考人类智能的独特之处。创造力、直觉和美学判断等能力可能成为人类区别于AI的关键特质。
知识获取的民主化
如果数学AI工具变得普及,可能会降低高级数学研究的门槛,使更多人能够参与数学发现。这将促进知识的民主化,但也可能带来新的不平等形式。
结论:AI与数学的新纪元
AlphaProof代表了AI在数学推理领域的重要里程碑,但它只是开始,而非终点。正如DeepMind团队所设想的,未来的数学AI将更加高效、强大,成为数学家不可或缺的助手。
"数学是一门需要创造力和严谨性的学科,"Hubert总结道,"我们的目标不是取代数学家,而是增强他们的能力,让他们能够探索更广阔的数学宇宙。"
随着技术的不断进步,我们可以期待看到AI与数学家之间更加紧密、高效的协作模式。这种协作不仅会加速数学发现,还可能帮助我们解决当前人类难以企及的复杂问题,从基础数学到应用科学,都将因此受益。
AlphaProof的故事告诉我们,人工智能与数学的结合正在开启一个充满可能性的新时代,在这个时代中,机器的计算能力与人类的创造力将携手前行,共同探索数学的无限奥秘。