基于MATLAB的均匀面阵MUSIC算法DOA估计仿真
在声呐、雷达等信号处理领域,波达方向(DOA)估计是一项至关重要的技术。它旨在确定空间信号源相对于阵列传感器的方向。MUSIC(Multiple Signal Classification)算法,作为一种经典的子空间算法,因其高分辨率和良好的性能而备受青睐。本文将深入探讨基于MATLAB的均匀面阵MUSIC算法的DOA估计仿真,揭示其背后的数学原理和实际应用。
MUSIC算法的理论基础
MUSIC算法属于特征结构子空间算法,其核心思想是将阵列接收到的数据协方差矩阵进行特征分解,从而得到信号子空间和噪声子空间。信号子空间由与信号相关的特征向量张成,而噪声子空间则由与噪声相关的特征向量张成。由于信号子空间和噪声子空间是正交的,因此可以通过搜索与噪声子空间正交的方向向量来估计信号的DOA。
对于均匀面阵,假设有$K$个远场窄带信号入射到由$M$个传感器组成的均匀面阵上。接收信号可以表示为:
$$ X(t) = A(\theta, \phi)S(t) + N(t) $$
其中,$X(t)$是$M \times 1$的接收信号向量,$A(\theta, \phi)$是$M \times K$的阵列流形矩阵,$S(t)$是$K \times 1$的信号向量,$N(t)$是$M \times 1$的噪声向量。$\theta$和$\phi$分别表示信号的方位角和俯仰角。
阵列流形矩阵$A(\theta, \phi)$的每一列对应于一个信号方向的导向矢量。对于均匀面阵,导向矢量可以表示为:
$$ a(\theta, \phi) = [e^{-j2\pi(x_m\cos(\theta)\cos(\phi) + y_m\sin(\theta)\cos(\phi)) / \lambda}]_{m=1}^{M} $$
其中,$x_m$和$y_m$是第$m$个传感器的坐标,$\lambda$是信号波长。
接收信号的协方差矩阵可以估计为:
$$ R_x = E[X(t)X^H(t)] = A(\theta, \phi)R_sA^H(\theta, \phi) + \sigma^2I $$
其中,$R_s$是信号的协方差矩阵,$\sigma^2$是噪声功率,$I$是单位矩阵。
对协方差矩阵$R_x$进行特征分解,可以得到$M$个特征值和对应的特征向量。将特征值从大到小排列,前$K$个较大的特征值对应的特征向量张成信号子空间,剩余的$M-K$个特征向量张成噪声子空间。噪声子空间可以表示为$U_n$。
MUSIC算法通过搜索以下谱函数来估计DOA:
$$ P_{MUSIC}(\theta, \phi) = \frac{1}{a^H(\theta, \phi)U_nU_n^Ha(\theta, \phi)} $$
谱函数的峰值对应于信号的DOA估计值。
MATLAB仿真步骤
阵列参数设置:
- 定义阵列类型(例如,均匀矩形阵列)。
- 设置阵元数量和阵元间距。
- 确定阵列的几何中心。
信号参数设置:
- 设置信号源的数量。
- 定义每个信号源的方位角和俯仰角。
- 设置信号频率和带宽。
- 生成信号波形(例如,正弦波或 chirp 信号)。
噪声参数设置:
- 设置噪声类型(例如,高斯白噪声)。
- 定义信噪比(SNR)。
数据生成:
- 根据阵列参数、信号参数和噪声参数,生成阵列接收到的数据。
- 可以使用MATLAB中的
randn函数生成高斯白噪声。
协方差矩阵估计:
- 使用接收到的数据估计协方差矩阵。
- 可以使用MATLAB中的
cov函数估计协方差矩阵。
特征分解:
- 对协方差矩阵进行特征分解,得到特征值和特征向量。
- 可以使用MATLAB中的
eig函数进行特征分解。
噪声子空间估计:
- 根据信号源的数量,选择合适的特征向量张成噪声子空间。
谱函数搜索:
- 在预定的角度范围内,计算MUSIC谱函数。
- 可以使用MATLAB中的
meshgrid函数生成角度网格。
DOA估计:
- 找到MUSIC谱函数的峰值,对应的角度即为DOA估计值。
- 可以使用MATLAB中的
max函数找到谱函数的峰值。
结果可视化:
- 将MUSIC谱函数绘制成图像,并标记DOA估计值。
- 可以使用MATLAB中的
plot、surf等函数进行可视化。
MATLAB仿真代码示例
以下是一个简单的MATLAB代码示例,用于演示基于均匀矩形阵列的MUSIC算法DOA估计:
% 阵列参数
M = 10; % 阵元数量
d = 0.5; % 阵元间距(以波长为单位)
% 信号参数
K = 2; % 信号源数量
theta = [30 60]; % 方位角(度)
phi = [45 45]; % 俯仰角(度)
f = 1; % 信号频率(归一化频率)
% 噪声参数
SNR = 10; % 信噪比(dB)
% 生成阵列流形矩阵
pos = (0:M-1)*d;
A = exp(-1j*2*pi*pos'*cosd(theta).*cosd(phi));
% 生成信号
N = 1000; % 快拍数
S = randn(K,N);
% 生成噪声
N0 = randn(M,N);
N0 = N0./norm(N0,'fro')*norm(A*S,'fro')*10^(-SNR/20);
% 接收信号
X = A*S + N0;
% 协方差矩阵估计
R = X*X'/N;
% 特征分解
[V,D] = eig(R);
[eigValue,index] = sort(diag(D),'descend');
U = V(:,index);
% 噪声子空间
Un = U(:,K+1:M);
% 角度搜索范围
theta_scan = -90:0.5:90;
phi_scan = -90:0.5:90;
% MUSIC谱函数
Pmusic = zeros(length(theta_scan), length(phi_scan));
for i = 1:length(theta_scan)
for j = 1:length(phi_scan)
a = exp(-1j*2*pi*pos'*cosd(theta_scan(i)).*cosd(phi_scan(j)));
Pmusic(i,j) = 1/(a'*Un*Un'*a);
end
end
% 结果可视化
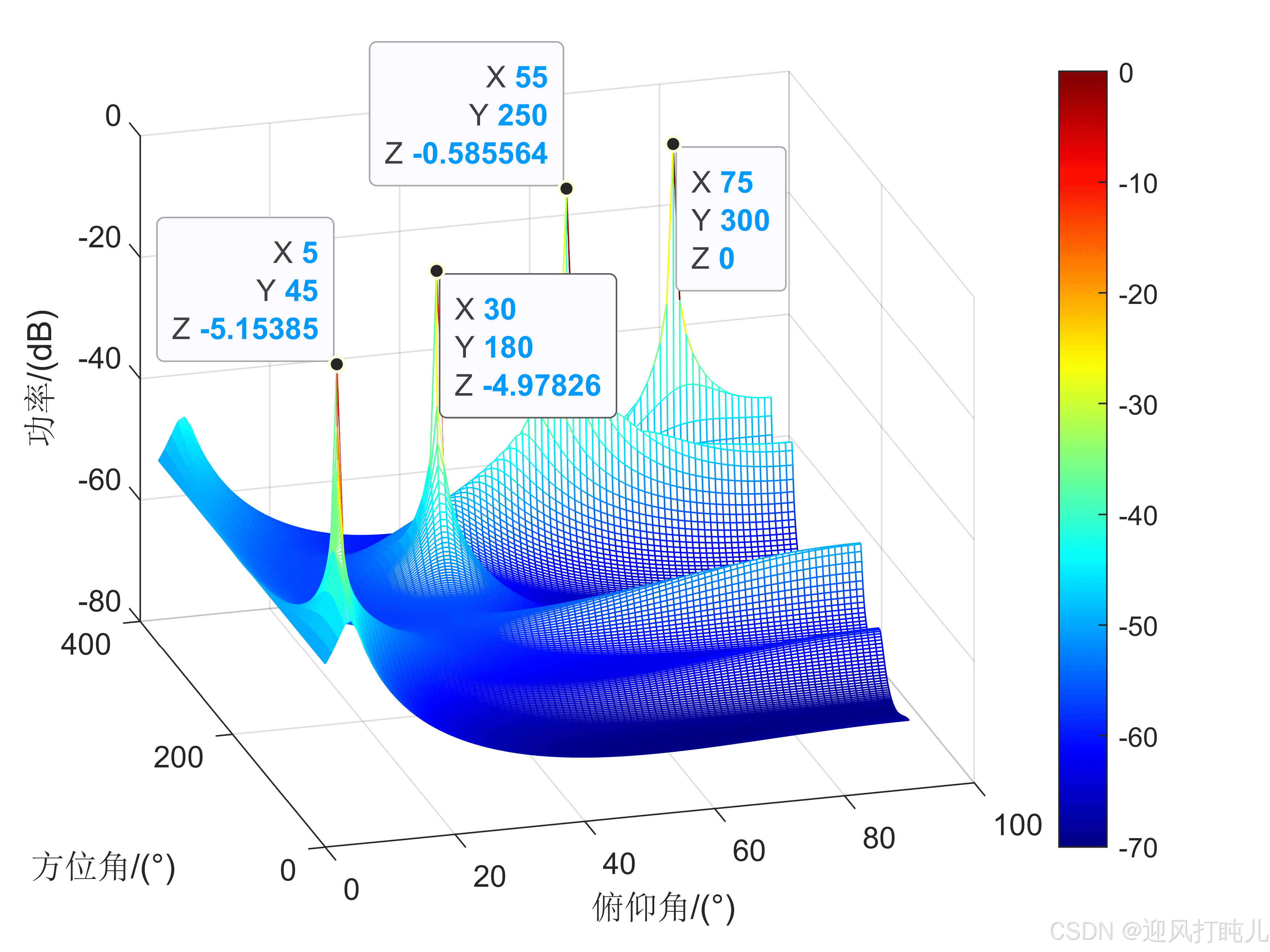
surf(theta_scan, phi_scan, 10*log10(abs(Pmusic)));
xlabel('方位角 (度)');
ylabel('俯仰角 (度)');
zlabel('MUSIC谱 (dB)');
title('基于均匀矩形阵列的MUSIC算法DOA估计');
shading interp
colormap jet
colorbar仿真结果分析
通过MATLAB仿真,可以得到MUSIC谱函数的图像。谱函数的峰值对应于信号的DOA估计值。通过比较估计值与真实值,可以评估MUSIC算法的性能。影响MUSIC算法性能的因素包括:
- 信噪比(SNR):SNR越高,DOA估计的准确性越高。
- 阵元数量:阵元数量越多,DOA估计的分辨率越高。
- 快拍数:快拍数越多,协方差矩阵估计的准确性越高。
- 信号源数量:MUSIC算法对信号源数量的估计精度有一定要求。如果信号源数量估计不准确,DOA估计的性能会下降。
结论与展望
本文详细介绍了基于MATLAB的均匀面阵MUSIC算法DOA估计的原理和仿真步骤。通过MATLAB仿真,可以深入理解MUSIC算法的性能,并为实际应用提供参考。随着信号处理技术的不断发展,DOA估计技术将在雷达、声呐、无线通信等领域发挥更加重要的作用。未来的研究方向包括:
- 高分辨率DOA估计:研究更高分辨率的DOA估计算法,以提高在复杂环境下的DOA估计性能。
- 宽带DOA估计:研究适用于宽带信号的DOA估计算法,以适应更广泛的应用场景。
- 自适应DOA估计:研究能够自适应调整参数的DOA估计算法,以提高在非理想条件下的DOA估计性能。
希望本文能够帮助读者更好地理解和应用MUSIC算法,为DOA估计技术的发展贡献力量。