人工智能领域再次迎来重大突破。谷歌正式推出Gemini 3 Deep Think模式,这一创新性解决方案专为Google AI Ultra订阅用户设计,标志着AI系统在推理能力方面的显著提升。这一发展不仅解决了当前AI模型在处理复杂问题时的局限性,更为人工智能在教育、科研和工程等领域的应用开辟了新的可能性。
推理能力的全新高度
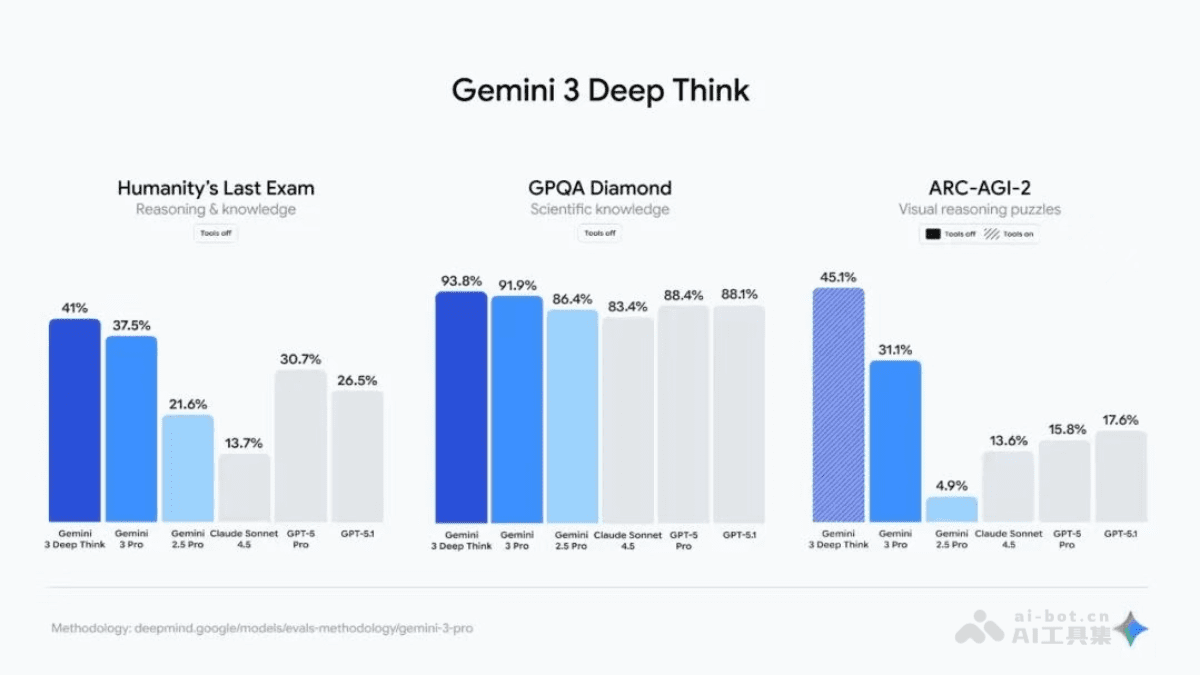
Gemini 3 Deep Think模式的核心价值在于其卓越的推理能力。与之前的版本相比,这一模式在处理复杂数学问题、科学计算和逻辑推理方面表现出色。谷歌通过先进的并行推理技术,使AI系统能够同时探索多个假设,从而更接近人类的思考方式。
在"人类最后的考试"这一严格基准测试中,Gemini 3 Deep Think未使用工具的情况下取得了41.0%的成绩,这是一个令人印象深刻的数字。更值得注意的是,在ARC-AGI-2测试中,当使用代码执行功能时,该模型更是达到了前所未有的45.1%的准确率。这些数据不仅证明了Gemini 3 Deep Think的技术实力,也为AI推理能力的未来发展指明了方向。

技术创新与并行推理
Gemini 3 Deep Think的成功源于其采用的先进并行推理技术。与传统的线性推理过程不同,这一模式能够同时考虑多种可能性,通过多路径探索寻找最优解决方案。这种创新方法使AI系统能够更接近人类的思维方式,特别是在处理需要创造性思维和复杂逻辑推理的问题时。
这一技术突破并非偶然。谷歌研发团队在Gemini 2.5 Deep Think的基础上进行了深入优化和改进。后者最近在国际数学奥林匹克竞赛和国际大学编程竞赛世界决赛中已经达到了金牌标准,而Gemini 3 Deep Think则在此基础上实现了质的飞跃。
实际应用场景与价值
Gemini 3 Deep Think的推出将为多个领域带来深远影响。在教育领域,这一模式可以辅助教师设计更具挑战性的教学内容,同时为学生提供个性化的学习指导。在科研方面,它能够加速复杂科学问题的解决过程,从药物研发到气候变化研究,AI推理能力的提升都将产生革命性影响。
此外,在工程设计和商业决策等领域,Gemini 3 Deep Think也能够提供更精准的分析和预测。通过处理复杂的逻辑关系和多重变量,这一模式可以帮助企业做出更明智的战略决策,优化运营流程,提高效率。
用户体验与可及性
对于Google AI Ultra订阅用户而言,Gemini 3 Deep Think的体验非常直观。用户只需在提示栏中选择"Deep Think"模式,并在模型下拉菜单中选择Gemini 3 Pro,即可立即体验这一强大功能。这种简化的操作流程确保了先进AI技术的可及性,使更多用户能够受益于推理能力的提升。
谷歌的这一举措也反映了AI技术发展的一个重要趋势:将复杂的AI功能以用户友好的方式呈现。通过降低使用门槛,谷歌不仅扩大了AI技术的应用范围,也为用户提供了更多探索和创造的可能性。
行业影响与未来展望
Gemini 3 Deep Think的推出将对整个AI行业产生深远影响。这一模式不仅展示了AI推理能力的最新进展,也为其他科技公司设定了新的技术标杆。可以预见,未来我们将看到更多专注于提升推理能力的AI模型出现,推动整个行业向更高水平发展。
从长远来看,Gemini 3 Deep Think所代表的并行推理技术可能会成为AI系统的标准配置。随着技术的不断成熟,我们有望看到AI在解决复杂问题方面取得更大突破,甚至在某些领域超越人类专家的能力。
技术挑战与伦理考量
尽管Gemini 3 Deep Think带来了令人振奋的进步,我们也必须认识到AI推理能力提升所伴随的挑战。随着AI系统处理更复杂问题的能力增强,如何确保决策的透明度和可解释性变得尤为重要。谷歌需要在这一领域持续投入研发,确保AI系统的决策过程能够被理解和信任。
此外,随着AI推理能力的提升,伦理问题也日益凸显。如何确保AI系统在处理敏感问题时遵循伦理准则,如何防止AI被用于不当目的,这些都是行业需要共同面对和解决的问题。
结论:迈向更智能的AI未来
Gemini 3 Deep Think的推出标志着AI推理能力的一个重要里程碑。通过并行推理技术和优化的算法,这一模式展示了AI在处理复杂问题方面的巨大潜力。随着技术的不断进步,我们有理由相信,AI将在更多领域发挥关键作用,为人类社会带来积极变革。
对于开发者和研究人员而言,Gemini 3 Deep Think提供了一个强大的工具,可以加速创新和应用开发。而对于普通用户来说,这一模式意味着更智能、更可靠的AI助手,能够帮助他们解决日常和工作中遇到的复杂问题。
展望未来,AI推理能力的提升将继续推动技术边界。随着Gemini 3 Deep Think和其他类似模型的发展,我们正迈向一个AI与人类协作解决全球性挑战的新时代。这一发展不仅将改变我们与技术互动的方式,也将深刻影响人类社会的未来发展路径。