在人工智能快速发展的今天,数学推理作为衡量AI深度思考能力的重要指标,一直是研究者们关注的焦点。DeepSeek-Math-V2的问世,为这一领域带来了革命性的突破。作为DeepSeek团队推出的开源数学推理模型,它不仅在多项国际顶级数学竞赛中展现出接近人类顶尖水平的解题能力,更通过创新的自我验证机制和协同进化训练方法,重新定义了AI在数学推理领域的可能性。
DeepSeek-Math-V2概述
DeepSeek-Math-V2是基于DeepSeek-V3.2-Exp-Base开发的开源数学推理模型,其核心特点是能够实现自我验证的数学推理。与传统的AI模型不同,DeepSeek-Math-V2不仅关注答案的正确性,更注重推理过程的严谨性。通过训练定理证明验证器和生成器,模型引入元验证机制,使其能够像人类数学家一样审查证明过程,甚至自我纠错。

在IMO(国际数学奥林匹克竞赛)、CMO(中国数学奥林匹克竞赛)和Putnam(普特南数学竞赛)等极具挑战性的数学竞赛基准上,DeepSeek-Math-V2的表现接近满分水平,证明了其在解决高难度数学问题上的卓越能力。这一成就不仅标志着AI在数学推理领域的重大进展,也为未来AI辅助数学研究和教育提供了新的可能性。
核心功能与技术原理
定理证明与自我验证
DeepSeek-Math-V2的核心功能之一是强大的定理证明能力。模型能够生成严谨的数学证明,适用于复杂的数学问题,如国际数学奥林匹克竞赛和普特南数学竞赛等高难度场景。更令人印象深刻的是,该模型具备自我验证能力,能够评估自身生成的证明过程,判断其正确性和严谨性,类似于人类数学家的自我检查过程。
这种自我验证机制通过"诚实奖励"实现。模型在生成答案后会进行自我评估,发现并修正错误,从而有效减少AI常见的幻觉问题。这种机制确保了模型不仅在结果上正确,在推理过程上也同样可靠,这对于数学这种高度依赖严谨逻辑的领域至关重要。
验证器与生成器架构
DeepSeek-Math-V2的技术架构基于创新的验证器-生成器协同进化模式。这一架构包含三个关键组件:
定理证明验证器(Proof Verifier):训练一个基于语言模型的验证器,专门用于评估数学证明的正确性和严谨性。验证器将证明分为三个等级:完美(1分)、有小瑕疵(0.5分)、有根本性错误(0分),并提供详细评语,帮助生成器改进。
证明生成器(Proof Generator):训练一个生成器,用于生成数学证明,并在生成后进行自我评估。生成器采用诚实奖励机制,鼓励模型在生成答案后诚实地指出自己的错误,从而获得更高奖励。
元验证(Meta-Verification):引入"督导"角色,对验证器的评估结果进行二次审查,避免验证器产生错误评估(如幻觉问题)。通过这种双重验证机制,确保模型对证明的评估更加准确和可信。
协同进化训练机制
DeepSeek-Math-V2最大的创新在于其"学生-老师-督导"的协同进化机制。在这一机制中,生成器和验证器相互作用,形成良性循环:
- 生成器不断生成新的证明,验证器对其进行评估
- 系统自动筛选出难以验证或难以解决的问题,作为新的训练数据
- 随着生成器能力的提升,扩展验证计算能力,自动标注新的难以验证的证明
- 生成更多训练数据,保持生成与验证之间的动态平衡
这种协同进化机制使得模型能够持续自我提升,不断突破数学推理能力的边界。与传统静态训练方法不同,DeepSeek-Math-V2的动态进化过程更接近人类学习数学的方式,通过不断挑战和解决更复杂的问题来提升能力。
性能表现与基准测试
DeepSeek-Math-V2在多个权威数学竞赛基准测试中展现出令人瞩目的性能,这些结果不仅证明了模型的实用性,也为AI数学推理能力提供了客观评估标准。
国际数学竞赛表现
IMO 2025(国际数学奥林匹克竞赛 2025):DeepSeek-Math-V2达到金牌水平,显示出在解决高难度数学证明题方面的强大能力。这一成绩意味着模型能够与人类顶尖数学竞赛选手相媲美。
CMO 2024(中国数学奥林匹克竞赛 2024):模型同样达到金牌水平,证明其不仅在国际竞赛中表现出色,在国内顶级数学竞赛中同样具有强大竞争力。
Putnam 2024(普特南数学竞赛 2024):在扩展测试计算的支持下,DeepSeek-Math-V2实现接近满分的成绩(118/120),这一分数已经接近人类顶尖选手的水平,充分展示了模型在高等数学领域的推理能力。
专项基准测试
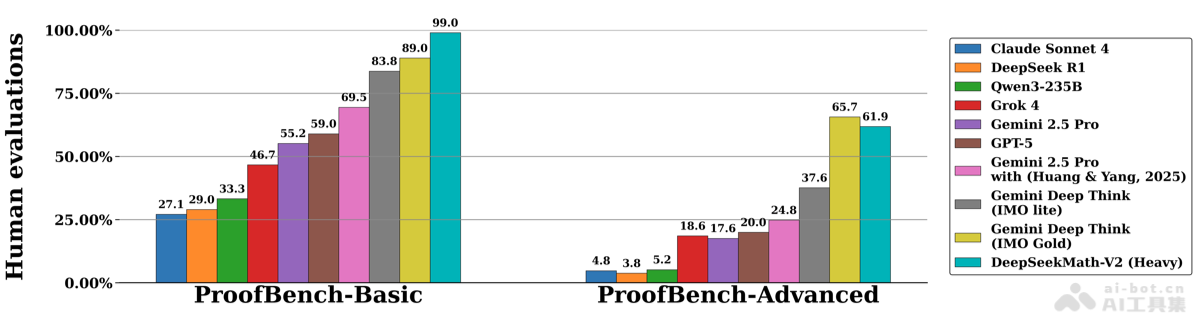
在IMO-ProofBench基准测试中,DeepSeek-Math-V2的表现同样令人印象深刻:
- Basic子集:达到接近99%的高分,远超其他模型,证明模型在基础数学证明任务上的卓越能力。
- Advanced子集:虽略逊于Gemini Deep Think(IMO Gold),仍然表现出色,说明在复杂证明题上仍有提升空间,但已达到世界领先水平。
这些测试结果表明,DeepSeek-Math-V2不仅能够解决常规数学问题,还能应对极具挑战性的高级数学推理任务,其能力已经接近甚至超越了许多人类数学专家。
应用场景与实际价值
DeepSeek-Math-V2的强大数学推理能力使其在多个领域具有广阔的应用前景,这些应用不仅能够提高工作效率,还能推动相关领域的发展和创新。
智能辅导与教育
在数学教育领域,DeepSeek-Math-V2可以作为智能辅导工具,帮助学生理解和生成数学证明,提供详细的解题步骤和逻辑分析。具体应用包括:
- 个性化学习:根据学生的学习进度和理解能力,提供定制化的数学证明指导,帮助学生逐步掌握复杂的数学概念。
- 解题思路分析:不仅给出答案,还能展示完整的推理过程,帮助学生理解每一步的逻辑依据。
- 错误纠正:识别学生在证明过程中的常见错误,提供针对性的改进建议,避免重复犯错。
- 竞赛训练:为参赛者提供高质量的练习题和解题思路,模拟竞赛环境,提升竞赛成绩。
这种智能辅导工具可以弥补传统教育中一对一辅导资源不足的问题,让更多学生能够获得高质量的数学指导。
数学研究与定理证明
对于专业数学家而言,DeepSeek-Math-V2可以作为强大的研究助手,在定理证明和数学研究方面发挥重要作用:
- 辅助证明:帮助数学家验证复杂定理的证明过程,发现潜在的逻辑漏洞,加速数学研究进程。
- 猜想验证:对数学猜想进行初步验证,为数学家提供研究方向和可能的证明路径。
- 文献分析:快速分析大量数学文献,找出相关研究和方法,帮助研究者把握领域前沿。
- 跨领域应用:将一个领域的数学方法应用到另一个领域,促进学科交叉创新。
这些应用可以大大提高数学研究的效率,让研究者能够将更多精力投入到创造性工作中,而不是繁琐的验证过程。
理论物理与工程应用
在理论物理和工程领域,DeepSeek-Math-V2可以辅助处理复杂的数学模型和公式推导:
- 物理模型验证:辅助物理学家推导复杂的数学公式和理论,验证物理模型的数学基础。
- 工程计算:在工程设计中解决复杂的数学优化问题,提高设计效率和准确性。
- 算法优化:帮助开发更高效的数学算法,应用于科学计算和工程实践。
- 数据分析:处理大规模科学数据,发现其中的数学规律和模式。
这些应用可以加速科学发现和技术创新,推动物理和工程领域的发展。
AI研究与基准测试
作为研究数学推理和逻辑验证的基准模型,DeepSeek-Math-V2在AI研究领域也具有重要价值:
- 推理能力研究:为研究AI的数学推理能力提供标准测试平台,推动深度推理算法的发展。
- 可解释AI:通过展示详细的推理过程,增强AI决策的可解释性,提高AI系统的透明度。
- 多模态学习:探索数学推理与其他AI能力的结合,推动多模态AI系统的发展。
- 安全与可靠性:研究如何提高AI系统的安全性和可靠性,特别是在关键决策中的应用。
这些研究将有助于推动AI向更高级的认知能力发展,实现从感知智能到认知智能的跨越。
技术优势与局限性
技术优势
自我验证机制:通过元验证和诚实奖励,模型能够自我检查和纠正错误,减少AI幻觉问题。
协同进化训练:验证器与生成器的协同进化使模型能够持续自我提升,不断突破能力边界。
开源特性:作为开源模型,DeepSeek-Math-V2允许研究人员和开发者自由使用、修改和改进,促进技术共享和协作创新。
高精度推理:在多个数学竞赛基准中接近满分水平,证明了其在复杂数学问题上的强大推理能力。
可解释性:模型提供详细的证明过程和评估结果,增强了AI决策的可解释性和透明度。
局限性与挑战
尽管DeepSeek-Math-V2取得了显著成就,但仍存在一些局限性和挑战:
计算资源需求:模型的训练和推理需要大量计算资源,限制了其在普通设备上的应用。
高级问题处理:在极其复杂的数学问题上,模型的表现仍有提升空间,特别是与人类顶尖数学家相比。
跨领域应用:虽然模型在数学领域表现出色,但将其能力扩展到其他领域仍面临挑战。
伦理与安全:随着AI能力的提升,如何确保其安全、负责任的使用成为重要课题。
可访问性:虽然模型是开源的,但普通用户可能缺乏使用和理解高级AI模型的技术能力。
这些局限性为未来的研究和改进指明了方向,也是推动AI技术持续发展的重要动力。
未来发展方向
基于DeepSeek-Math-V2的成功和当前面临的挑战,未来的研究和发展可能集中在以下几个方向:
计算效率优化:降低模型训练和推理的计算资源需求,使其能够在更广泛的设备上运行。
多模态扩展:将数学推理能力与其他感知和认知能力结合,开发更全面的多模态AI系统。
领域适应性增强:提高模型在不同数学分支和领域的适应性,扩展其应用范围。
人机协作模式:开发更有效的人机协作模式,让AI能够更好地辅助人类专家的工作。
伦理与安全框架:建立完善的伦理和安全框架,确保AI技术的负责任发展和应用。
教育应用深化:开发更多针对教育场景的应用,让AI技术更好地服务于数学教育。
这些发展方向将进一步推动AI在数学推理领域的能力提升,扩大其应用范围和影响力。
结论
DeepSeek-Math-V2的出现标志着AI在数学推理领域取得了重大突破。通过创新的自我验证机制和协同进化训练方法,该模型在多项国际顶级数学竞赛中展现出接近人类顶尖水平的解题能力,证明了AI在深度推理方面的巨大潜力。
作为开源模型,DeepSeek-Math-V2不仅为研究人员提供了宝贵的研究工具,也为教育、科研、工程等多个领域带来了新的可能性。从智能辅导到定理证明,从理论物理到AI研究,其应用前景广阔,有望推动多个领域的创新和发展。
尽管仍存在一些局限性和挑战,但随着技术的不断进步和完善,DeepSeek-Math-V2及其后续模型将在AI辅助数学研究和教育中发挥越来越重要的作用。这一技术的进步不仅将改变我们学习和研究数学的方式,也将推动人工智能向更高级的认知能力发展,开启AI深度推理的新篇章。